Matemática

1) A figura abaixo foi dividida em dois quadrados e dois retângulos. Escreva o que é pedido em cada item:

a) O Polinômio que representa a área de cada retângulo;

b) O Polinômio que representa a área do quadrado maior;

c) O Polinômio que representa a área do quadrado maior;

d) O Polinômio que representa a área total da figura.

2) Uma das aplicações dos produtos notáveis é para facilitar alguns cálculos numéricos que, aparentemente, seria complicado realizar sem calculadora. Faça os cálculos por meio dos produtos notáveis e depois confira os resultados com uma calculadora, se possível.

a) 33²

b) 58²

c) 41.39

3) Para cada figura, escreva uma expressão reduzida que represente a medida da área colorida:

4) Uma lâmina quadrada de alumínio tem no seu interior uma perfuração quadrada, cujas dimensões aparecem na figura. Determine a expressão simplificada que representa a área não perfurada.

5) Um dos pavimentos da casa de Victor é uma linda sala, que seria quadrada se não fosse um pequeno jardim de inverno situado num canto dela. Dê o polinômio que representa:
a) a área desse pavimento;
b) a área do jardim de inverno;
c) a área da sala.

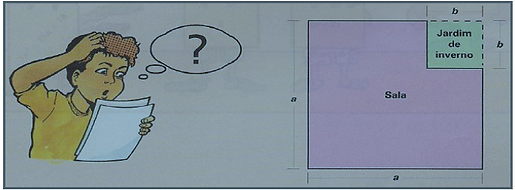
6) A expressão algébrica que representa a situação: “o quadrado da soma de dois números, mais cinco unidades” é:

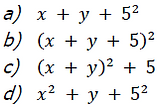
7) A fatoração do polinômio 2x(x + 1) + (x + 1) = é:

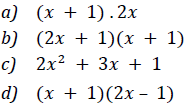
8) Desenvolva os produtos notáveis a seguir:

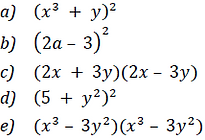
9) Desenvolva os produtos notáveis e reduza os termos semelhantes:

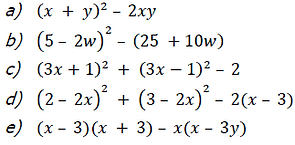
10) Sabendo que A + B = 8 e que A – B = 2 determine o valor de:

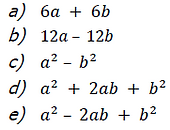
11) Usando as regras de produtos notáveis, descubra o valor de x na igualdade:

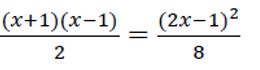
12) Desafio:

a) Sabendo que X + Y = 10 e que XY = 6 , determine o valor de X² + Y² . (Dica: eleve x + y ao quadrado).

b) Sabendo que X² + Y² = 25 e que XY = 12 , descubra o valor de (X + Y )²

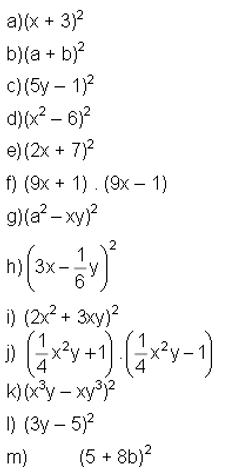
13) Utilizando as regras dos produtos notáveis, calcule:

Mas há uma outra razão que explica a elevada reputação das Matemáticas, é que elas levam as ciências naturais exatas uma certa proporção de segurança que, sem elas, essas ciências não poderiam obter.

"Albert Einstein"

Exercícios 7ª Série - Produtos Notáveis

14) Desenvolva os produtos notáveis:

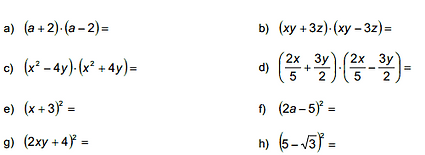
15) Calcule o valor das expressões abaixo:

16) Usando produtos notáveis, calcule:

17) Calcule:

a) (3 + x)² = ( R: 9 + 6x +x²)

b) (x + 5)² = ( R: x² + 10x + 25)

c) ( x + y)² = ( R: x² + 2xy +y²)

d) (x + 2)² = ( R: x² + 4x + 4)

e) ( 3x + 2)² = ( R: 9x² + 12x +4)

f) (2x + 1)² = (R: 4x² + 4x + 1)

g) ( 5+ 3x)² = (R: 25 + 30x + 9x²)

h) (2x + y)² = (R: 4x² + 4xy + y²)

i) (r + 4s)² = (R: r² + 8rs + 16s²)

j) ( 10x + y)² = (R: 100x² + 20xy + y²)

l) (3y + 3x)² = (R: 9y² + 18xy + 9x²)

m) (-5 + n)² = (R: 25 -10n + n²)

n) (-3x + 5)² = (R: 9x² - 30x + 25)

o) (a + ab)² = (R: a² + 2a²b + a²b²)

p) (2x + xy)² = (R: 4x² + 4x²y + x²y²)

q) (a² + 1)² = (R: (a²)² + 2a² + 1)

r) (y³ + 3)² = [R: (y³)² + 6y³ + 9]

s) (a² + b²)² = [R: (a²)² + 2a²b² + (b²)²]

t) ( x + 2y³)² = [R: x² + 4xy³ + 4(y³)²]

u) ( x + ½)² = (R: x² +x + 1/4)

v) ( 2x + ½)² = (R: 4x² + 2x + 1/4)

x) ( x/2 +y/2)² = [R: x²/4 + 2xy/4 + y²/4]