
Matemática
O céu deve ser necessariamente esférico, pois a esfera, sendo gerada pela rotação do círculo, é, de todos os corpos, o mais perfeito.
Exercícios 6ª Série - Equações do 1º Grau
01) Encontre o valor de X que satisfaça a igualdade imposta pelas seguintes equações:
Resolução: Clique aqui.
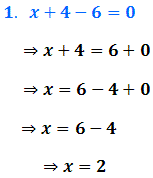
02) Passemos ao exercicio seguinte em que a variavel X está presente em ambos os termos da equação.
Resolução: Clique aqui.

03) Vamos agora aumentar um pouco a dificuldade na próxima equação, as operações seram as mesmas somente adições e subtracções.
Resolução: Clique aqui.

04) A este ponto; introduzimos equações que incluam multiplicações e/ou divisões.
Resolução: Clique aqui.

05) Introduziremos algumas fracções na equação seguinte, postaremos a resolução segundo 2 métodos de resolução:
Resolução: Clique aqui.

06) No exercício seguinte, iremos efectuar os calculos segundo a variavel y, ao invês da usualmente utilizada variavel x.
Não existe diferença em calcular segundo variavel x, y, z, ou a.
Qualquer uma das letras do alfabeto pode servir de variavel de calculo, o procedimento para resolução não altera em nada!!!
Resolução: Clique aqui.

07) Resolva as equações
Respstas: Clique aqui.
a) x+30 = 40 b) 30-20+2x=10 c) 3x-10+13=-2x+28 d) 20x-30=40+30-20
e) -5x+45-89=-90+41 f) 10x-20=40+50 g) 20-80+2x=10 h) 19+2x-13=10-20
i) 10x-12+10=+18-20 l) 13x-23-45=-7x+12 m) x – 3 = 7 n) x + 4 = 10
o) x + 101 = 300 p) x – 279 = 237 q) x – 8 = –10 r) x + 9 = –1
s) 3x = 12 t) 9x = 18 u) 35x = –105 v) 7x – 1 = 13
x) 6x – 10 = 2x + 14 y) 6x = 2x + 28 z) 3(x + 2) = 15 a1) 2(x – 1) – 7 = 16
b1) 7(x – 2) = 5(x + 3) c1) 2(x – 6) = –3(5 + x)
05) Resolva as equações






a2) x + 5 = 8 ( R = 3) b2) x - 4 = 3 (R = 7) c2) x + 6 = 5 ( R = -1)
d2) x -3 = - 7 (R= -4) e2) x + 9 = -1 (R=-10) f2) x + 28 = 11 (R=-17)
g2) x - 109 = 5 (R= 114) h2) x - 39 = -79 (R=-40) i2) 10 = x + 9 (R=2)
j2) 15 = x + 20 (R= -5) l2) 4 = x - 10 ( R= 14) m2) 7 = x + 8 ( R= -1)
n2) 0 = x + 12 (R= -12) o2) -3 = x + 10 (R= -13)
a3) 3x = 15 (R=5) b3) 2x = 14 ( R=7) c3) 4x = -12 (R=-3)
d3) 7x = -21 (R=-3) e3) 13x = 13 (R= 1) f3) 9x = -9 (R=-1)
g3) 25x = 0 (R=0) h3) 35x = -105 (R=-3) i3) 4x = 1 (R=1/4)
j3) 21 = 3x (R=7) l3) 84 = 6x (R=14) m3) x/3 =7 (R=21)
n3) x/4 = -3 (R=-12) o3) 2x/5 = 4 (R=10) p3) 2x/3 = -10 (R=-15)
q3) 3x/4 = 30 (R=40) r3) 2x/5 = -18 (R= -45)
06) Resolva as equações
